Frequenzberechnung
Die Änderung der potentiellen Energie $V$ der Kerne kann durch eine Taylor-Reihe um Entwicklungspunkt $X_0$ ausgedrückt werden:
\[V(X) = V(X_0) + g^T(X-X_0) + \frac{1}{2}(X-X_0)^T H (X-X_0) + ...\]wobei wiederum $g$ der Gradient und $H$ die Hesse-Matrix ist. Die harmonische Näherung vereinfacht diese Taylor-Reihe indem nur die Terme bis zur zweiten Ableitung berücksichtigt werden. Im Energie-Minimum ist der Gradient $g^T=0$ und mit der Wahl $V(X_0)=0$ ergibt sich:
\[V(X) = \frac{1}{2}(X-X_0)^T H (X-X_0)\]Die Elemente der Hesse-Matrix sind die zweiten Ableitungen der potentiellen Energie nach den Kernpositionen. Durch Diagonalisierung (Ähnlichkeitstransformation) wechselt man in das Koordinatensystem der Normalmoden und die Hesse-Matrix wird zur Diagonalmatrix $\Lambda$. Die Beiträge einzelner Atomkerne gehen hierbei massegewichtet in die Hesse-Matrix ein. Die Eigenwerte $\lambda_i$ entsprechen den Kraftkonstanten und können in Schwingungsfrequenzen $\nu_i$ umgerechnet werden:
\[\nu_i = \frac{1}{2\pi} \sqrt{\frac{\lambda_i}{\mu}}\]Wird diese harmonische Näherung korrekt auf eine Minimums-Geometrie angewandt so sind alle Eigenwerte reell und positiv.
Falls ein Sattelpunkt vorliegt sind einige Eigenwerte negativ und die entsprechenden Frequenzen imaginär.
Folgende Abbildung zeigt die ersten drei Normalmoden des Wassermoleküls. Diese entsprechen der antisymmetrischen- und symmetrischen Streckschwingung, sowie der Biegeschwingung.
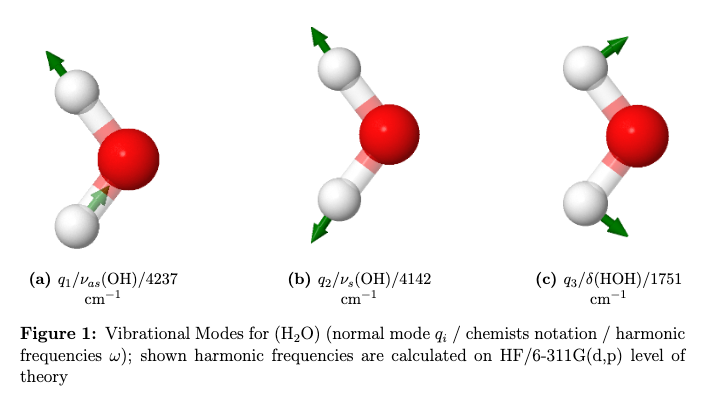
Frequenzberechnung in Orca
Folgender Input-File ist ein Beispiel für eine Frequenzberechnung in Orca. Als Methode wird wiederum Hartree Fock mit dem 6-311G(d,p) Basissatz verwendet.
!HF 6-311G(d,p) OPT FREQ
* xyz 0 1
H 0.000000000 1.415075762 0.956290882
O 0.000000000 0.000000000 -0.120510070
H 0.000000000 -1.415075762 0.956290882
*
Es wird sowohl eine Geometrie-Optimierung (OPT) als auch eine Frequenzberechnung (FREQ) durchgeführt. Grundsätzlich kann die Frequenzberechnung analytisch (wenn verfügbar) oder numerisch (durch z.B. Finite-Differenzen) durchführt werden.
-----------------------
VIBRATIONAL FREQUENCIES
-----------------------
Scaling factor for frequencies = 1.000000000 (already applied!)
0: 0.00 cm**-1
1: 0.00 cm**-1
2: 0.00 cm**-1
3: 0.00 cm**-1
4: 0.00 cm**-1
5: 0.00 cm**-1
6: 1750.79 cm**-1
7: 4141.74 cm**-1
8: 4237.00 cm**-1
------------
NORMAL MODES
------------
These modes are the Cartesian displacements weighted by the diagonal matrix
M(i,i)=1/sqrt(m[i]) where m[i] is the mass of the displaced atom
Thus, these vectors are normalized but *not* orthogonal
0 1 2 3 4 5
0 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000
1 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000
2 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000
3 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000
4 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000
5 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000
6 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000
7 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000
8 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000
6 7 8
0 -0.000000 -0.000000 -0.000000
1 -0.430096 -0.583118 -0.561293
2 0.559049 -0.398411 -0.427118
3 0.000000 0.000000 0.000000
4 -0.000000 0.000001 0.070729
5 -0.070445 0.050202 -0.000001
6 -0.000000 0.000000 0.000000
7 0.430096 0.583097 -0.561316
8 0.559049 -0.398396 0.427133
Im Output-File findet man dann die berechneten Frequenzen in $\text{cm}^{-1}$ und die zugehörigen massegewichteten Normalmoden.
Anharmonische Frequenzberechnung mit VPT2
Vibrational pertubation theroy (VPT) ist eine möglichkeit um die harmonische Beschreibung von molekularen Schwingungen zu verbessern. Man kann also die Anharmonizität der Schwingung berücksichtigen. Diese ist allgemein definiert als die Abweichung der experimentellen Schwingungsfrequenzen von den harmonischen Frequenzen.
In der VPT2-Methode wird der Hamiltonian in einen nullten-Ordnung teil $H^{(0)}$ und Störungsterme $H^{(1)}$ und $H^{(2)}$ usw. zerlegt. Für den nullten-Ordnung Teil sind die exakten Eigenfunktionen hierbei bekannt, zudem wird angenommen das die Störungsterme klein sind. Grundsätzlich wird VPT2 mittels des Watson-Hamiltonians formuliert, welcher die Kopplung zwischen Rotation und Vibration berücksichtigt. Dieser Hamiltonian ist in Normalkoordinaten $Q_i$ ausgedrückt, welche bereits in der Aufgabe der harmonischen Frequenzberechnung eingeführt wurden.
Der nullte-Ordnungsterm korrespondiert hierbei mit der harmonischen Näherung, während die Störungsterme anharmonische Beiträge enthalten. Um die Anharmonizität der PES zu beschreiben wird dieses als semi-quartic force-field (QFF) ausgedrückt.
\[V = \frac{1}{2} \sum \lambda_i Q_i² + \frac{1}{6} \sum F_{ijk} Q_i Q_j Q_k + \frac{1}{24} \sum F_{ijkl} Q_i Q_j Q_k Q_l\]Hierbei sind $F_{ijk}$ und $F_{ijkl}$ die kubischen und quartischen Ableitungen des Potentials mit der Form:
\[F_{ijk} = \frac{\partial^3 V}{\partial Q_i \partial Q_j \partial Q_k}\] \[F_{ijkl} = \frac{\partial^4 V}{\partial Q_i \partial Q_j \partial Q_k \partial Q_l}\]Es sei hier angemerkt, dass VPT2 nur den Beginn der anharmonischen Schwingungskorrekturen darstellt und eine Vielzahl weiterer Methoden existiert. Für den interessierten Leser hier eine Liste an Literatur:
VPT2 in Orca
Zuerst einige wichtige Hinweise zur Verwendung von VPT2 in Orca:
- Die Startgeometrie muss strikte Konvergenzkriterien erfüllen. Hierfür kann man in Orca die Option
!TightOptoder! VeryTightOptverwenden. - Zudem sollte man mit einer vorherigen harmonischen Frequenzberechnung sicherstellen, dass die Geometrie einem Minimum entspricht.
- Das SCF muss striktere Konvergenzkriterien erfüllen. Dazu verwendet man am besten
!ExtremeSCFoder!VeryTightSCF. - VPT2 in Orca funktioniert nur für nicht-lineare Moleküle.
Folgender Block zeigt einen typischen Input für eine VPT2-Rechnung in Orca für das Wassermolekül:
! RHF 6-311G(d,p) ExtremeSCF VPT2
%pal nprocs 4 end
%vpt2
VPT2 On
HessianCutoff 1e-12
PrintLevel 1
end
%method
Z_Tol 1e-14
end
* xyz 0 1
O 0.10579950836185 0.00000000000000 0.00000000000000
H 0.70570224581907 0.00000000000000 0.74668419232728
H 0.70570224581908 0.00000000000000 -0.74668419232728
*
Es müssen Methoden mit analytischer Hesse-Matrix verwendet werden, z.B. HF. Zudem kann man im Code-Block %vpt2 die Parameter für die VPT2-Rechnung einstellen. Es wurde ein Cut-Off für die Elemente der Hesse-Matrix von $1 \times 10^{-12}$ gewählt um numerische Ungenauigkeiten zu vermeiden. Die Option Z_Tol im Block %method legt eine striktere Konvergenzbedingung für die CP-SCF-Rechnung fest.
===================== Vibrational Analysis =====================
Anharmonic constants [1/cm]
---------------------------
r s chi[r][s]
---------------------------
0 0 -15.29924
1 0 -8.20737
1 1 -40.73760
2 0 -21.57456
2 1 -160.26486
2 2 -45.24153
---------------------------
Fundamental transitions [1/cm]
-----------------------------------------
Mode w(harm) v(fund) Diff
-----------------------------------------
0 1821.363 1775.873 -45.489
1 3922.027 3756.316 -165.711
2 3990.137 3808.734 -181.403
-----------------------------------------
Zero-point ro-vibrational energy [1/cm]
---------------------------------------
Harmonic contribution: 4866.763
Anharmonic correction: -72.831
Ro-vibrational correction: 4.718
---------------------------------------
Total: 4798.650
Overtones and combination bands
--------------------------------------------------------------------------------
modes freq eps Int T**2 ( Tx Ty Tz )
[cm-1] [L/(mol*cm)] [km/mol] [a.u.]
--------------------------------------------------------------------------------
0 0 3521.15 0.000104 0.52 0.000009 (-0.000000 -0.003031 0.000000)
0 1 5523.98 0.000010 0.05 0.000001 (-0.000000 -0.000755 -0.000000)
0 2 5563.03 0.000706 3.57 0.000040 ( 0.006291 -0.000000 -0.000000)
1 1 7431.16 0.000157 0.80 0.000007 ( 0.000000 -0.002571 -0.000000)
1 2 7404.78 0.000732 3.70 0.000031 ( 0.005552 -0.000000 -0.000000)
2 2 7526.98 0.000042 0.21 0.000002 (-0.000000 -0.001324 -0.000000)
============================== End =============================
Im oberen Block findet man die jeweiligen anharmonischen Frequenzen $v_{fund}$ und die Differenz zur harmonischen Frequenz. Zudem erhält man die Obertöne und Kombinationsbanden mit den jeweiligen Frequenzen und Intensitäten.
Aufgabe 2a
Berechnen Sie die harmonischen Frequenzen für alle Moleküle ihrer Reaktion und vergleiche Sie diese mit experimentellen Daten. Machen Sie sich bewusst um welche Art von Experiment es sich handelt. Verwenden Sie für die Berechnung die folgenden Methoden-Basissatz Kombinationen:
- HF/6-311G(d,p)
- B3LYP/6-311G(d,p)
- MP2/6-311G(d,p)
Wichtig!!
In Orca sind für die MP2-Methode keine analytischen zweiten Ableitungen (Hesse-Matrix) implementiert. Daher muss die Hesse-Matrix numerisch über Finite-Differenzen berechnet werden. Dies kann durch die Angabe der Option numfreq im Input-File erreicht werden.
Aufgabe 2b
Berechnen Sie die anharmonischen VPT2 Frequenzen mittels der HF Methode und dem 6-311G(d,p) Basissatz. Wie groß sind die Unterschiede zwischen harmonischen und anharmonischen Frequenzen? Handelt es sich bei den VPT2-Frequenzen um gekoppelte oder entkoppelte Vibrationszustände?
Verständnisfragen
- Wie erkennt man anhand der harmonischen Schwingungsfrequenzen ob ein Energie-Minimum oder ein Sattelpunkt vorliegt?
- Was sind Normalmoden? Wie werden diese berechnet und konstruiert?
- Wie kommt man von den Eigenwerten der Hesse-Matrix zu den Schwingungsfrequenzen?
- Welche Möglichkeiten gibt es für anharmonische Korrekturen der Schwingungsfrequenzen?
- Wie funktioniert die VPT2-Methode? Wie funktioniert das Analogon der Elektronenstrukturtheorie (Störungstheorie)?
- Warum unterscheiden sich harmonische Frequenzen so stark von den experimentellen Werten? Welche Effekte werden in der harmonischen Näherung nicht berücksichtigt?
- Wie viele Vibrationsmoden hat ein Molekül mit $N$ Atomen?
- Wie beurteilt man ob eine Schwingung IR-aktiv ist?
- Was sind Obertöne und Kombinationsbanden?