Optimierung der Molekülgeometrie
Eine dreidimensionale Anordnung von Atomen im Raum ist eine Molekülgeometrie. Die Minimumsgeometrie ist jene wo die potentielle Energie des Moleküls minimal ist. Für viele quantenchemische Berechnungen ist das Auffinden einer Minimumsgeometrie oft der erste Schritt. Dies wird als Geometrieoptimierung bezeichnet.
Folgende Abbildung (erstellt von Prof. Thomas Hofer) zeigt schematisch eine Geometrieoptimierung. Beginnend von einer Startgeometrie soll die relative Anordnung der Atomkerne zueinander gefunden werden, sodass die Gesamtenergie des Moleküls minimal ist. In dieser Anordnung sind die Kräfte die auf die Atomkerne wirken gleich Null.
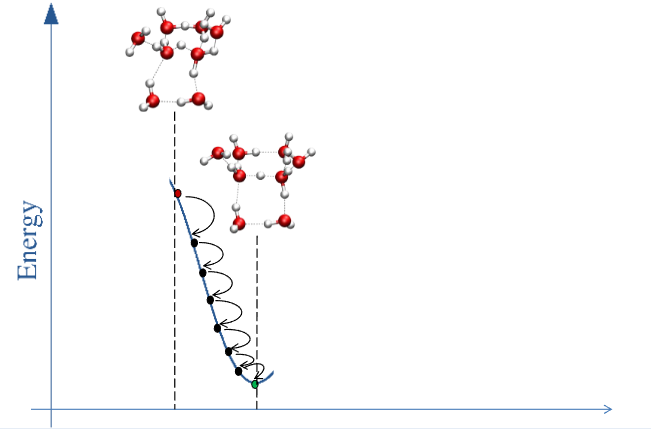
Note: Jede Anordnung der Kerne entspricht einen Punkt auf der Potential-Hyperfläche (engl. Potential Energy Surface, PES). Diese Fläche beschreibt die potentielle Energie des Moleküls in Abhängigkeit der Kernpositionen. Eine Geometrieoptimierung sucht den nächstgelegenen Tiefpunkt auf dieser Fläche.
Die Potentialhyperfläche ist unbekannt kann jedoch mathematisch als Taylor-Reihe approximiert werden:
\[E(x) = E(x_0) + g_0^T \Delta x + \frac{1}{2} \Delta x^T H_0 \Delta x + ...\]- $g_0^T$ ist der Gradient und entspricht der ersten Ableitung der Energie nach den Kernpositionen. Im Minimum ist dieser Vektor gleich Null.
- $H_0$ ist die Hesse-Matrix und entspricht der zweiten Ableitung der Energie nach den Kernpositionen. Diese Matrix beschreibt die Krümmung der Potential-Hyperfläche
Geometrie-Optimierung in Orca
Folgender Input-File ist ein Beispiel für eine Geometrieoptimierung in Orca.
! HF 6-311G(d,p) OPT
* xyz 0 1
O 0.000000 0.000000 0.000000
H 0.758602 0.000000 0.504284
H 0.758602 0.000000 -0.504284
*
Die erste Zeile beginnend mit dem ! Symbol enthält hier die Anweisungen für Orca:
- HF: Verwendung der Hartree-Fock Methode
- 6-311G(d,p): Spezifikation des Basissatzes
- OPT: Keyword für die Geometrieoptimierung
Die Zeilen mit dem *xyz beschreiben die Geometrie des Moleküls in Räumlichen Koordinaten. Die 0 und 1 geben die Gesamtladung und Multiplizität des Moleküls an.
Ein Blick in den Output-File
Im Output-File wird folgender Block angezeigt wann die Geometrie-Optimierung beginnt:
*****************************
* Geometry Optimization Run *
*****************************
Geometry optimization settings:
Update method Update .... BFGS
Choice of coordinates CoordSys .... (2022) Redundant Internals
Initial Hessian InHess .... Almloef's Model
Max. no of cycles MaxIter .... 50
Convergence Tolerances:
Energy Change TolE .... 5.0000e-06 Eh
Max. Gradient TolMAXG .... 3.0000e-04 Eh/bohr
RMS Gradient TolRMSG .... 1.0000e-04 Eh/bohr
Max. Displacement TolMAXD .... 4.0000e-03 bohr
RMS Displacement TolRMSD .... 2.0000e-03 bohr
Strict Convergence .... False
Dieser Block zeigt sowohl die Optimierungsmethode (BFGS) als auch die Wahl der Koordinaten (Redundant Internals) und einige Parameter für die Konvergenz des Verfahrens.
.--------------------.
----------------------|Geometry convergence|-------------------------
Item value Tolerance Converged
---------------------------------------------------------------------
RMS gradient 0.1118954640 0.0001000000 NO
MAX gradient 0.1618216140 0.0003000000 NO
RMS step 0.1732050808 0.0020000000 NO
MAX step 0.2739217962 0.0040000000 NO
-------------------------------------------------------------------------
........................................................
Max(Bonds) 0.0458 Max(Angles) 15.69
Max(Dihed) 0.00 Max(Improp) 0.00
---------------------------------------------------------------------
The optimization has not yet converged - more geometry cycles are needed
Nach des jeweiligen SCF-Runs wird dann ein Block angezeigt welcher die aktuelle Konvergenz des Verfahrens beschreibt. Dieser zeigt beispielsweise die aktuelle Step-Length sowie den Gradienten und die Toleranzparameter welche in der Anfangsphase meist nicht erfüllt sind.
.--------------------.
----------------------|Geometry convergence|-------------------------
Item value Tolerance Converged
---------------------------------------------------------------------
Energy change -0.0000268592 0.0000050000 NO
RMS gradient 0.0002059687 0.0001000000 NO
MAX gradient 0.0002093130 0.0003000000 YES
RMS step 0.0006471653 0.0020000000 YES
MAX step 0.0010850366 0.0040000000 YES
-------------------------------------------------------------------------
........................................................
Max(Bonds) 0.0001 Max(Angles) 0.06
Max(Dihed) 0.00 Max(Improp) 0.00
---------------------------------------------------------------------
The step convergence is overachieved with
reasonable convergence on the gradient
Convergence will therefore be signaled now
***********************HURRAY********************
*** THE OPTIMIZATION HAS CONVERGED ***
*************************************************
Sobald die Optimierungskriterien erfüllt sind wird dieser Block im Output-File angezeigt. Man erhält somit eine Minimumsgeometrie welche man für weitere Berechnungen verwenden kann.
Aufgabe 1
Berechnen Sie optimierte Strukturen für die Moleküle der Ihnen zugewiesenen Reaktion auf den nachfolgenden Levels of Theory:
- HF/6-311G(d,p)
- B3LYP/6-311G(d,p)
- MP2/6-311G(d,p)
Vergleichen Sie im Anschluss die internen Koordinaten Ihrer Moleküle mit experimentellen Daten. Stellen Sie sich die Frage ob dieser Vergleich notwendig ist oder ob eine ähnliche Aussage bereits früher anhand der berechneten Energien getroffen werden kann?
Verständnisfragen
- Was bestimmt das Ende einer Geometrieoptimierung?
- Welche Rolle spielt der Gradient in einer Geometrieoptimierung?
- Wie könnte ich sehen ob eine Geometrieoptimierung ein Minimum gefunden hat (Stichwort: Frequenzberechnung)?
- Was ist die Hesse-Matrix und welche Information enthält diese?
- Woher kommen hochgenaue experimentelle Geometriedaten von kleinen Molekülen.